二次函数解析式综合题求法例举
二次函数解析式的求法是二次函数知识的重点,也是中考必考内容。本文试以历年中考题为例,说明求二次函数解析式的常用方法,以期对同学们学习有所帮助。
二次函数常见的表达形式有:
(1)一般式: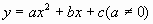 ;
;
(2)顶点式: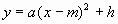 ,其中点(m,h)为该二次函数的顶点;
,其中点(m,h)为该二次函数的顶点;
(3)交点式: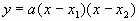 ,其中点
,其中点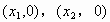 为该二次函数与x轴的交点。
为该二次函数与x轴的交点。
例1. 已知抛物线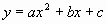 经过A,B,C三点,当
经过A,B,C三点,当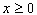 时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
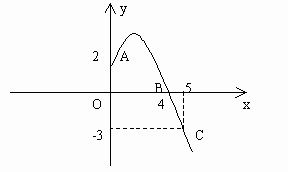
图1
分析:由图象可知,抛物线经过A(0,2),B(4,0),C(5,-3)三点,因此,可以借助二次函数一般式求出其解析式,再转化为顶点式,求出顶点坐标。
解:设所求抛物线的解析式为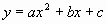 (
(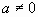 )。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
)。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
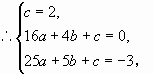 解之,得
解之,得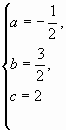
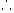 抛物线的解析式为
抛物线的解析式为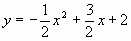
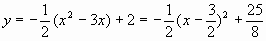
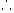 该抛物线的顶点坐标为
该抛物线的顶点坐标为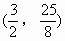 。
。
点评:这道题的一个特点是题中没有直接给出所求抛物线经过的点的坐标,需要从图象中获取信息。已知图象上三个点时,通常应用二次函数的一般式列方程求解析式。要特别注意:如果这道题是求图象所表示的函数解析式,那就必须加上自变量的取值范围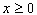 。
。
例2. 如图2,有一横截面是抛物线的水渠,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,标杆有1m浸没在水中,露出水面的部分与水面成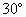 的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
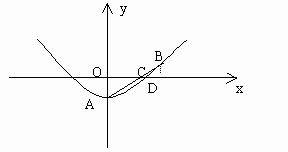
图2
分析:要求解析式,必须知道抛物线上交点的坐标。显然,由已知条件可以求出点A与点B的坐标。由于点A是所在抛物线的顶点,因此可以用抛物线的顶点式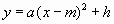 。
。
解:设AB与x轴交于点C,可知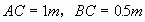 。
。
过点B作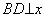 轴于点D
轴于点D
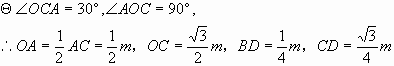
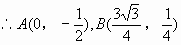
设所求水渠横截面抛物线的解析式为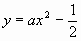 。
。
将点B的坐标代入,有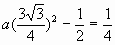 。解之,得
。解之,得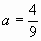 。
。
因此,该水渠横截面抛物线的解析式为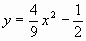 。
。
点评:解答此类问题的关键在于将实际问题的条件转化成点的坐标,再根据点的特征选择适当的函数表达式。
例3. 一条抛物线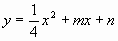 经过点
经过点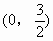 与
与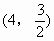 。求这条抛物线的解析式。
。求这条抛物线的解析式。
分析:解析式中的a值已经知道,只需求出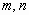 的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点
的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点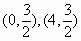 的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线
的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线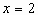 ,这样又可以从抛物线的顶点式入手。
,这样又可以从抛物线的顶点式入手。
解: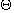 抛物线
抛物线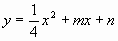 经过点(
经过点(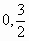 )和
)和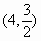 ,
,
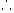 这条抛物线的对称轴是直线
这条抛物线的对称轴是直线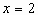 。
。
设所求抛物线的解析式为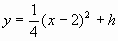 。
。
将点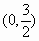 代入,得
代入,得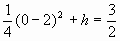 ,解得
,解得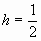 。
。
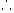 这条抛物线的解析式为
这条抛物线的解析式为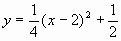 ,即
,即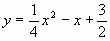 。
。
点评:当点M(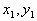 )和N(
)和N(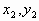 )都是抛物线上的点时,若
)都是抛物线上的点时,若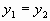 ,则对称轴方程为
,则对称轴方程为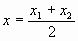 ,这一点很重要也很有用。
,这一点很重要也很有用。
例4. 如图3,在直角坐标系中,以点A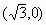 为圆心,以
为圆心,以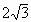 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线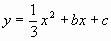 经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
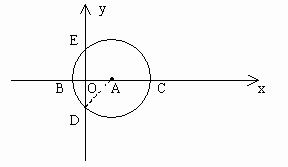
图3
分析:解题的关键在于求出点B和点C的坐标,因此需要求出线段OB,OC的长,这可根据圆的性质解决。由于点B与点C都在x轴上,因而可以根据二次函数的交点式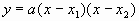 求出其解析式。
求出其解析式。
解:由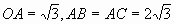 ,易得
,易得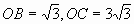
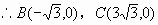
在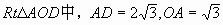 ,
,
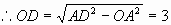 。所以点D的坐标为(0,-3)。
。所以点D的坐标为(0,-3)。
设解析式为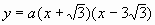 ,由条件知
,由条件知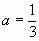 ,
,
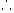 抛物线的解析式为
抛物线的解析式为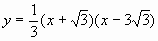
即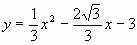
当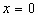 时,
时,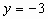 ,所以点D(0,-3)在抛物线上。
,所以点D(0,-3)在抛物线上。
点评:解这类题将点的坐标与线段的长互相转化至关重要,但要注意坐标的符号。
最后,留两道题给同学们练习。
1. 二次函数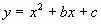 的图象经过点M(1,-2),N(-1,6)。求二次函数
的图象经过点M(1,-2),N(-1,6)。求二次函数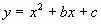 的关系式。 (答案:
的关系式。 (答案: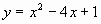 )
)
2. 已知抛物线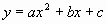 与y轴的交点为C,顶点为M,直线CM的解析式为
与y轴的交点为C,顶点为M,直线CM的解析式为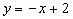 ,线段CM的长为
,线段CM的长为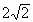 。求这条抛物线的解析式。(答案:
。求这条抛物线的解析式。(答案: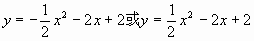 )
)
二次函数解析式的求法是二次函数知识的重点,也是中考必考内容。本文试以历年中考题为例,说明求二次函数解析式的常用方法,以期对同学们学习有所帮助。
二次函数常见的表达形式有:
(1)一般式: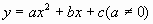 ;
;
(2)顶点式: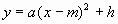 ,其中点(m,h)为该二次函数的顶点;
,其中点(m,h)为该二次函数的顶点;
(3)交点式: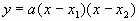 ,其中点
,其中点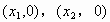 为该二次函数与x轴的交点。
为该二次函数与x轴的交点。
例1. 已知抛物线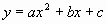 经过A,B,C三点,当
经过A,B,C三点,当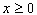 时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
时,其图象如图1所示。求抛物线的解析式,写出顶点坐标。
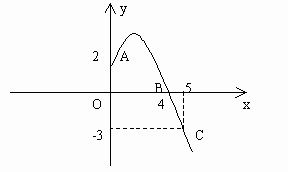
图1
分析:由图象可知,抛物线经过A(0,2),B(4,0),C(5,-3)三点,因此,可以借助二次函数一般式求出其解析式,再转化为顶点式,求出顶点坐标。
解:设所求抛物线的解析式为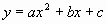 (
(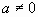 )。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
)。由图象可知A,B,C的坐标分别为(0,2),(4,0),(5,-3)。
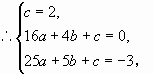 解之,得
解之,得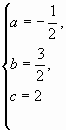
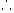 抛物线的解析式为
抛物线的解析式为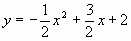
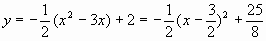
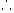 该抛物线的顶点坐标为
该抛物线的顶点坐标为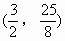 。
。
点评:这道题的一个特点是题中没有直接给出所求抛物线经过的点的坐标,需要从图象中获取信息。已知图象上三个点时,通常应用二次函数的一般式列方程求解析式。要特别注意:如果这道题是求图象所表示的函数解析式,那就必须加上自变量的取值范围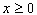 。
。
例2. 如图2,有一横截面是抛物线的水渠,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,标杆有1m浸没在水中,露出水面的部分与水面成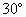 的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
的夹角(标杆与抛物线的横截面在同一平面内)。以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图2所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号)。
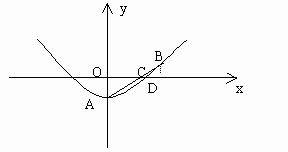
图2
分析:要求解析式,必须知道抛物线上交点的坐标。显然,由已知条件可以求出点A与点B的坐标。由于点A是所在抛物线的顶点,因此可以用抛物线的顶点式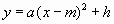 。
。
解:设AB与x轴交于点C,可知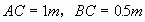 。
。
过点B作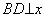 轴于点D
轴于点D
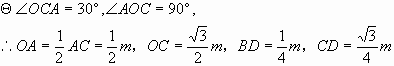
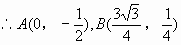
设所求水渠横截面抛物线的解析式为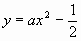 。
。
将点B的坐标代入,有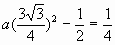 。解之,得
。解之,得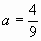 。
。
因此,该水渠横截面抛物线的解析式为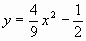 。
。
点评:解答此类问题的关键在于将实际问题的条件转化成点的坐标,再根据点的特征选择适当的函数表达式。
例3. 一条抛物线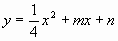 经过点
经过点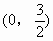 与
与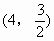 。求这条抛物线的解析式。
。求这条抛物线的解析式。
分析:解析式中的a值已经知道,只需求出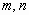 的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点
的值。已知条件给出了两个点,因此,可以从二次函数的一般式入手列方程组解答。还可以从所给两点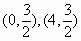 的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线
的特征入手:这两点关于抛物线的对称轴对称,因此可知对称轴是直线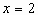 ,这样又可以从抛物线的顶点式入手。
,这样又可以从抛物线的顶点式入手。
解: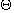 抛物线
抛物线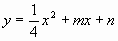 经过点(
经过点(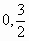 )和
)和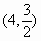 ,
,
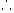 这条抛物线的对称轴是直线
这条抛物线的对称轴是直线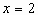 。
。
设所求抛物线的解析式为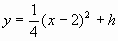 。
。
将点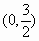 代入,得
代入,得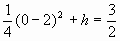 ,解得
,解得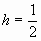 。
。
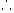 这条抛物线的解析式为
这条抛物线的解析式为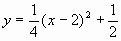 ,即
,即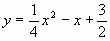 。
。
点评:当点M(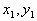 )和N(
)和N(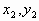 )都是抛物线上的点时,若
)都是抛物线上的点时,若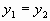 ,则对称轴方程为
,则对称轴方程为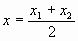 ,这一点很重要也很有用。
,这一点很重要也很有用。
例4. 如图3,在直角坐标系中,以点A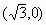 为圆心,以
为圆心,以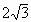 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E。若抛物线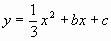 经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
经过B,C两点,求抛物线的解析式,并判断点D是否在抛物线上。
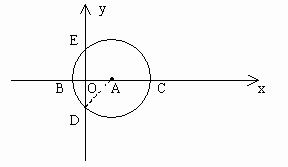
图3
分析:解题的关键在于求出点B和点C的坐标,因此需要求出线段OB,OC的长,这可根据圆的性质解决。由于点B与点C都在x轴上,因而可以根据二次函数的交点式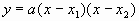 求出其解析式。
求出其解析式。
解:由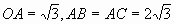 ,易得
,易得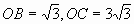
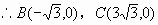
在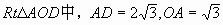 ,
,
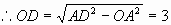 。所以点D的坐标为(0,-3)。
。所以点D的坐标为(0,-3)。
设解析式为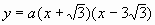 ,由条件知
,由条件知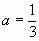 ,
,
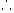 抛物线的解析式为
抛物线的解析式为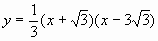
即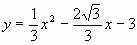
当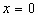 时,
时,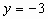 ,所以点D(0,-3)在抛物线上。
,所以点D(0,-3)在抛物线上。
点评:解这类题将点的坐标与线段的长互相转化至关重要,但要注意坐标的符号。
最后,留两道题给同学们练习。
1. 二次函数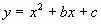 的图象经过点M(1,-2),N(-1,6)。求二次函数
的图象经过点M(1,-2),N(-1,6)。求二次函数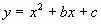 的关系式。 (答案:
的关系式。 (答案: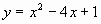 )
)
2. 已知抛物线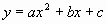 与y轴的交点为C,顶点为M,直线CM的解析式为
与y轴的交点为C,顶点为M,直线CM的解析式为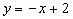 ,线段CM的长为
,线段CM的长为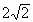 。求这条抛物线的解析式。(答案:
。求这条抛物线的解析式。(答案: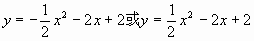 )
)
【二次函数解析式综合题求法例举】相关文章:
相关推荐
网友关注
- 2020年重庆高考报名时间为11月9日至18日_
- 2020武汉市中考获取分配生的考生及注意事项
- 2020郑州九中校园足球屡次“征战”海外
- 2020武汉市中考体育:3步轻松应对坐位体前屈
- 教育部:两项国家语委语言文字规范11月1日正式实施_
- 2019年11月,这些新规将开始实施,快来关注!_
- 2020武汉市中考体育:中长跑训练指南(含男生女生)
- 国管公积金简化提取申请材料,不再提交纸质申请书_
- 2020江苏省震泽中学招生简章(苏州重点高中)
- 2020武汉市中考体育:快速提高立定跳远秘诀
- 武汉七一华源中学公布“无作业日”实施方案
- 2020济南市各校美术生特长生招生计划公布
- 2020河南省中考英语考试题型变化解读
- 2020届高校毕业生预计达874万,教育部:确保就业稳定_
- 陕西扩大高职院校奖学金覆盖面,提高助学金标准_
网友关注视频
- 2019河北中考物理多选题 滑轮组的复合问题讲解 较难
- 中考英语
- 中考英语
- 中考英语
- 中考英语
- 暑假中考物理第9次课
- 2019年北京中考地理卷真题解析1
- 初中美术
- VLOG | 音乐节 | 海边 | 中考完后的日子
- 中考英语
- 【中考语文】总复习
- 2019下半年教师资格证笔试
- 2019年北京中考生物真题解析3
- 高考:最后三天,毛坦厂中学宣誓,学生舍不得班主任程晓东
- 十秒解决一个物理问题! 中考物理作图题! 必考!
- 七年级下册英语书人教版2017全国中考英语真题
- 2019年北京中考历史卷真题解析6
- 英语课本七年级上册北京中考英语真题初二英语单项选择题
- 今年中考作文写“作品” 语文老师分析:“虚实”合度巧立意
- 中考英语
- 中考作文热门主题及高分指导
- 速报!2019年北京中考语文试题专家解析来了 涵盖三大特点
- 十八岁的天空:高三全班故意考差想让班主任难堪,班主任这番话,让大家无地自容!
- 中考完的第一期视频(素材是6月23号中考完当天拍的)音乐喷泉
- 中考英语
- 中考英语
- 人教版化学中考总复习《化学变化的基本特征》课堂教学实录-韩彦霞
- 中考英语
- 中考英语
- 教师资格面试试讲示范——初中美术《对比色与邻近色》
精品推荐
- 2020中山市今天下午16时中考成绩公布及普高各批次安排
- 2020佛山中考成绩查询系统开通(附往年录取分数线)
- 2020深圳中考成绩通过四种方式查询
- 2020广东中山中考成绩8月5日16:00公布(附录取时间)
- 2020厦门中考成绩8月5日公布(附各科等级划分线标准)
- 2020沈阳8月4号中考成绩查询官网:www.sysksy.cn
- 2020上海市新高一新生报到·分班考·通知书寄送时间安排
- 2020福建南平市中考8月8日左右成绩查询人口:http://cjcx.npkmkj.net/
- 2020大连市成绩查询官网入口:http://dlzsks.edu.dl.gov.cn/
- 2020黄冈中考成绩查询官网:http://gzjd.hubzs.com.cn
