中考常见“实际问题与二次函数”类型题
运用二次函数的有关知识解决实际问题,是中考的热点之一,例如求销售利润的最值问题、几何图形变换中建立函数关系式的问题、以抛物线形为基础的实际问题都需要在实际的情景中去理解、分析所给的一系列数据,舍弃与解题无关的因素,建立数学模型。下面就几种常见的实际问题与二次函数类型题谈谈解题思路和方法。
一、最大利润问题
例1.某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进行了调查统计,得到如下数据:
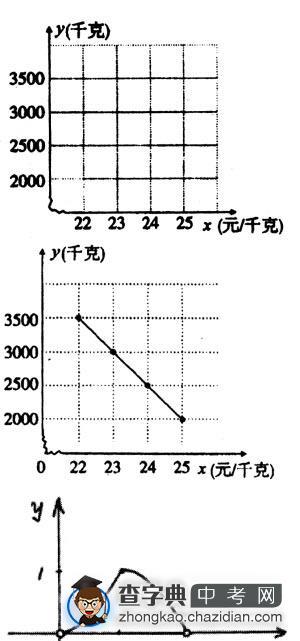
(1)在如图的直角坐标系内,做出各组有序数对(x,y)所对应的点。连接各点并观察所得的图形,判断y与x之间的函数关系,并求出y与x之间的函数关系式;
(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x(元/千克)之间的函数关系式,并求出当x取何值时,P的值最大?
分析:(1)正确描点、连线后,根据直线上两个点的坐标,可求出销售量y与销售单价x的关系式。
(2)销售利润(P)=销售量(y)单个产品的利润,将(1)结果代入后得,销售利润P为以x为自变量的二次函数,求出当x取何值时,P的值最大即求抛物线顶点横坐标。
解:(1)正确描点、连线。由图象可知,y是x的一次函数,设y=kx+b
∵点(25,2000)、(24,2500)在图象上
y=-500x+14500
(2)P=(x-13)y=(x-13)(-500x+14500)=-500x2+21000x-188500=-500(x-21)2+32000
P与x的函数关系式为P=-500x2+21000x-188500
当销售价为21元/千克时,能获得最大利润。
小结:解决此题要弄清楚题目中的数量关系,总销售额=销售量销售单价,总销售利润=销售量单个产品的利润(或总销售利润=总销售额-总成本),单件产品的利润=销售单价-产品成本。若求最大利润P值,即为求二次函数顶点纵坐标,P的最大值为32000元。
二、几何图形变换问题
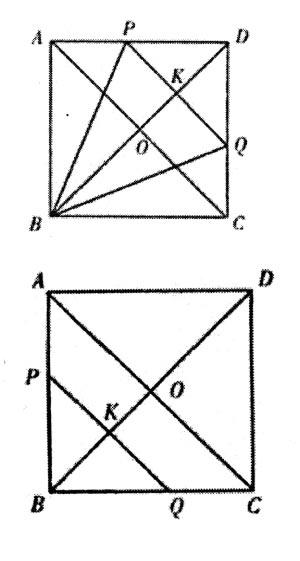
例2.已知:如图,正方形ABCD的边长为-,在对角线BD上有一动点K,过K作PQ∥AC并交正方形的两边于P、Q,设BK=x,S△BPQ=y。
求:(1)y关于x的函数关系式;
(2)画出函数图象。
分析:本题先分析出K点运动过程中,会出现两种不同情形的△BPQ,当K在BO上运动时,△BPQ为等腰直角三角形;
当K在OD上运动时,△DPQ为等腰直角三角形,而△BPQ仅为等腰三角形,故需要分两种情况讨论。
解:(1)设AC与BD相交于O
①当K在OB上时,△BPQ为等腰直角三角形
∵PBK=QBK=45
K为PQ中点
PQ=2BK=2x
y=-x2x=x2
(0
②当K在OD上运动时,△DPQ为等腰直角三角形
KD=2-x PQ=2(2-x)
y=-x2(2-x),y=-x2+2x (1x<2)
所求的函数关系式为
(2)函数图象如图所示
小结:几何变换问题在解题时,可能随着变换产生不同形状的几何图形,那么需要根据实际情况将结果用分段函数来表示,并注明相应自变量的取值范围。画图象时也应注意在自变量取值范围内,图象的变化趋势。
(周三继续刊登)
,解得:
2000=25k+b
2500=24k+b
{
k=-500
b=14500
{
y=
x2 (0
-x2+2x (1x<2)
{


运用二次函数的有关知识解决实际问题,是中考的热点之一,例如求销售利润的最值问题、几何图形变换中建立函数关系式的问题、以抛物线形为基础的实际问题都需要在实际的情景中去理解、分析所给的一系列数据,舍弃与解题无关的因素,建立数学模型。下面就几种常见的实际问题与二次函数类型题谈谈解题思路和方法。
一、最大利润问题
例1.某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进行了调查统计,得到如下数据:
(1)在如图的直角坐标系内,做出各组有序数对(x,y)所对应的点。连接各点并观察所得的图形,判断y与x之间的函数关系,并求出y与x之间的函数关系式;
(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x(元/千克)之间的函数关系式,并求出当x取何值时,P的值最大?
分析:(1)正确描点、连线后,根据直线上两个点的坐标,可求出销售量y与销售单价x的关系式。
(2)销售利润(P)=销售量(y)单个产品的利润,将(1)结果代入后得,销售利润P为以x为自变量的二次函数,求出当x取何值时,P的值最大即求抛物线顶点横坐标。
解:(1)正确描点、连线。由图象可知,y是x的一次函数,设y=kx+b
∵点(25,2000)、(24,2500)在图象上
y=-500x+14500
(2)P=(x-13)y=(x-13)(-500x+14500)=-500x2+21000x-188500=-500(x-21)2+32000
P与x的函数关系式为P=-500x2+21000x-188500
当销售价为21元/千克时,能获得最大利润。
小结:解决此题要弄清楚题目中的数量关系,总销售额=销售量销售单价,总销售利润=销售量单个产品的利润(或总销售利润=总销售额-总成本),单件产品的利润=销售单价-产品成本。若求最大利润P值,即为求二次函数顶点纵坐标,P的最大值为32000元。
二、几何图形变换问题
例2.已知:如图,正方形ABCD的边长为-,在对角线BD上有一动点K,过K作PQ∥AC并交正方形的两边于P、Q,设BK=x,S△BPQ=y。
求:(1)y关于x的函数关系式;
(2)画出函数图象。
分析:本题先分析出K点运动过程中,会出现两种不同情形的△BPQ,当K在BO上运动时,△BPQ为等腰直角三角形;
当K在OD上运动时,△DPQ为等腰直角三角形,而△BPQ仅为等腰三角形,故需要分两种情况讨论。
解:(1)设AC与BD相交于O
①当K在OB上时,△BPQ为等腰直角三角形
∵PBK=QBK=45
K为PQ中点
PQ=2BK=2x
y=-x2x=x2
(0
②当K在OD上运动时,△DPQ为等腰直角三角形
KD=2-x PQ=2(2-x)
y=-x2(2-x),y=-x2+2x (1x<2)
所求的函数关系式为
(2)函数图象如图所示
小结:几何变换问题在解题时,可能随着变换产生不同形状的几何图形,那么需要根据实际情况将结果用分段函数来表示,并注明相应自变量的取值范围。画图象时也应注意在自变量取值范围内,图象的变化趋势。
(周三继续刊登)
,解得:
2000=25k+b
2500=24k+b
{
k=-500
b=14500
{
y=
x2 (0
-x2+2x (1x<2)
{
【中考常见“实际问题与二次函数”类型题】相关文章:
相关推荐
网友关注
- 华师一录取工作时间和流程,要去的注意了!
- 武汉省级示范高中昨日开录考生 最早今晚可查结果
- 武汉省武昌实验中学的三限生开始收费了
- 2014年武汉一中新生录取通知公布
- 武汉各校拿录取通知书时间和军训时间汇总
- 2014年武汉十五中招生信息贴出
- 2014年武汉水果湖高中新高一录取名单
- 2014年武汉中考 7月4日16:00前考生可申请复查卷面分
- 2014年武汉二中三限生缴费通知
- 2014年武汉中考武珞路详细分数段
- 2014年华科附中高中录取名单公布
- 2014年武汉市各校三限生缴费通知(不断更新)
- 2014年武汉汉铁高中高一新生录取名单
- 武汉各区保底高中及相关录取政策介绍
- 2014年武汉市青山区中考前10名
网友关注视频
- 2019河北中考物理大题 杠杆定理和压强的综合题
- 十八岁的天空:高三全班故意考差想让班主任难堪,班主任这番话,让大家无地自容!
- 中考英语
- 暑假中考物理第10次课
- 2019年北京中考历史卷真题解析(3)
- 语文三轮复习课程_中考作文热门主题及高分指导
- 中考英语
- 中考英语
- 2019江苏淮安中考物理前五道选择题 开篇的几道选择题一般为送分题,难度不大,切莫丢分
- 小黎微课·2019中考物理一轮复习
- 中考英语
- 2019广州中考作文名师点评《别担心,我可以》
- 英语课本七年级上册2017河北省中考英语试题及答案
- 英语课本七年级下册初一英语测试2017泰州中考英语试卷
- 中考英语
- 中考英语
- 中考语文
- 2019年北京中考地理卷真题解析1
- 2019年北京中考生物真题解析4
- 初中美术
- 2019年北京中考生物真题解析1
- 中考完的第一期视频(素材是6月23号中考完当天拍的)音乐喷泉
- 今年中考作文写“作品” 语文老师分析:“虚实”合度巧立意
- 中考语文
- 【中考物理】武汉中考物理,电路选择压轴,究竟是什么难度
- 英语课本七年级下册七年级英语试题2017北京中考英语试卷
- 中考英语
- 2019年北京中考地理卷真题解析3
- 中考英语
- 中考英语
精品推荐
- 2020中山市今天下午16时中考成绩公布及普高各批次安排
- 2020佛山中考成绩查询系统开通(附往年录取分数线)
- 2020深圳中考成绩通过四种方式查询
- 2020广东中山中考成绩8月5日16:00公布(附录取时间)
- 2020厦门中考成绩8月5日公布(附各科等级划分线标准)
- 2020沈阳8月4号中考成绩查询官网:www.sysksy.cn
- 2020上海市新高一新生报到·分班考·通知书寄送时间安排
- 2020福建南平市中考8月8日左右成绩查询人口:http://cjcx.npkmkj.net/
- 2020大连市成绩查询官网入口:http://dlzsks.edu.dl.gov.cn/
- 2020黄冈中考成绩查询官网:http://gzjd.hubzs.com.cn
